Проба
![]()
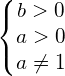
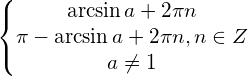
![Rendered by QuickLaTeX.com \[ \begin{bmatrix} \arcsin a + 2 \pi n \\ \pi - \arcsin a + 2 \pi n , n \in Z \end{bmatrix} \]](https://mileta.su/wp-content/ql-cache/quicklatex.com-690c80af8f44a9e437d4d0888718ac8e_l3.png)
![]()
После вылета со скоростью ![]() под углом
под углом ![]() (альфа) к горизонту тело одновременно совершает два движения: равноускоренное относительно оси
(альфа) к горизонту тело одновременно совершает два движения: равноускоренное относительно оси ![]() и равномерное относительно оси
и равномерное относительно оси ![]() .
.
Относительно оси ![]() движение происходит с ускорением
движение происходит с ускорением ![]() и начальной скоростью
и начальной скоростью ![]() :
:
![]()
Для движения относительно ![]() справедливы формулы равноускоренного движения:
справедливы формулы равноускоренного движения:
![]()
![]()