Векторные величины
Векторные величины в физике применяются в тех случаях, когда при их суммировании приходится учитывать не только размер, но и направление. Например, результат сложения двух последовательных перемещений зависит не только от их величины, но и от того, в каком направлении выполнены перемещения, следовательно перемещение является вектором. Результат сложения двух масс зависит только от их величины, может быть найдет единственным способом, следовательно масса является скалярной величиной, а не векторной.
К векторным величинам относятся: перемещение ![]() , скорость
, скорость ![]() , ускорение
, ускорение ![]() , сила
, сила ![]() , импульс
, импульс ![]() , напряженность поля
, напряженность поля ![]() , магнитная индукция
, магнитная индукция ![]() и другие величины.
и другие величины.
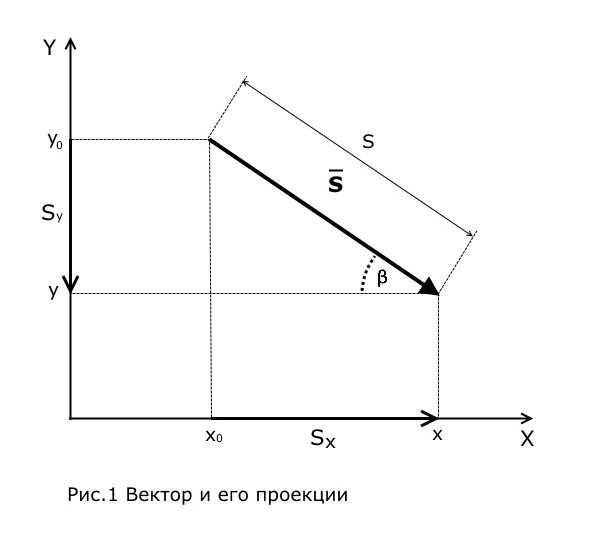
Характеристики вектора (рис.1):
1) ![]() модуль вектора — положительное число, равное длине вектора;
модуль вектора — положительное число, равное длине вектора;
2) ![]() угол наклона вектора — угол между прямой, проходящей через вектор и выбранной осью (на рис.1 осью X);
угол наклона вектора — угол между прямой, проходящей через вектор и выбранной осью (на рис.1 осью X);
3) ![]() проекция вектора — число, равное длине «тени» вектора со знаком «+» или «-» . Знак «+» ставится, если «тень» сонаправлена с осью координат и знак «-» ставится, если «тень» противоположно направлена оси координат.
проекция вектора — число, равное длине «тени» вектора со знаком «+» или «-» . Знак «+» ставится, если «тень» сонаправлена с осью координат и знак «-» ставится, если «тень» противоположно направлена оси координат.
Нахождение модуля и проекций вектора :
1) Проекцию вектора можно найти через его координаты, для этого от координаты конца вектора нужно отнять координату начала вектора:
![]()
![]()
2) Проекцию вектора можно найти с помощью угла, для этого модуль вектора нужно умножить на косинус прилежащего или синус противолежащего угла:
![]()
![]()
3) Модуль вектора можно найти через его проекции по теореме Пифагора:
![]()
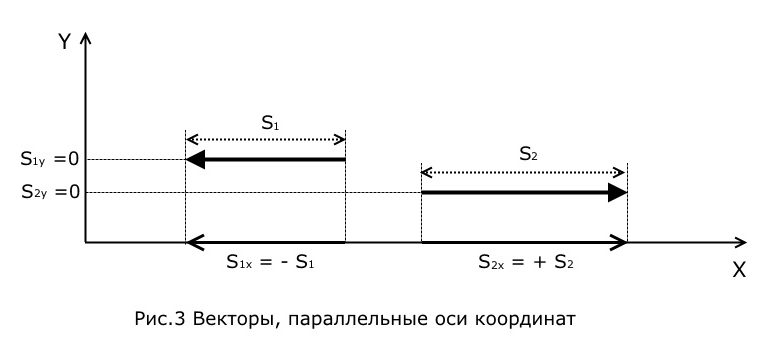
Проекции векторов, параллельных оси координат:
1) Если вектор ![]() противоположно направлен оси координат (рис.3), то его проекция на эту ось равна модулю вектора со знаком «-» :
противоположно направлен оси координат (рис.3), то его проекция на эту ось равна модулю вектора со знаком «-» :
![]()
2) Если вектор ![]() сонаправлен с осью координат (рис.3), то его проекция на эту ось равна модулю вектора со знаком «+» :
сонаправлен с осью координат (рис.3), то его проекция на эту ось равна модулю вектора со знаком «+» :
![]()
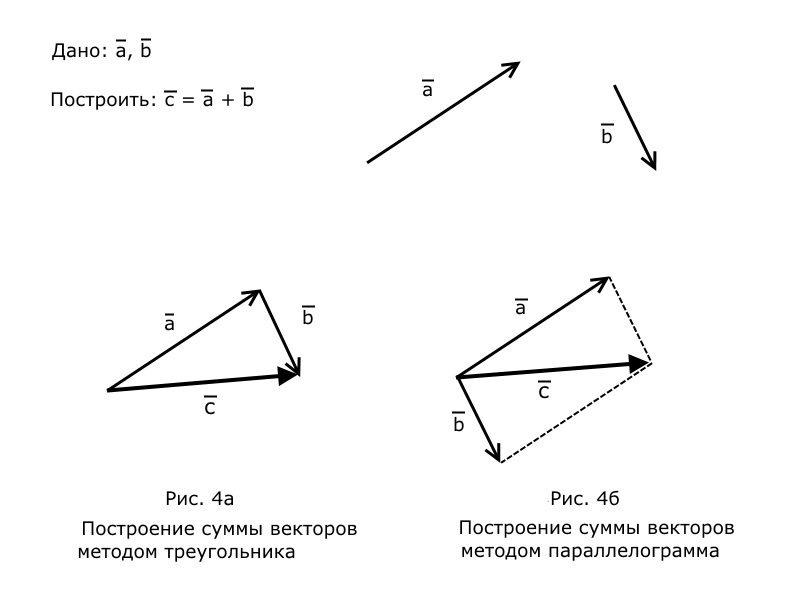
Сложение двух векторов методом треугольника (рис.4а). Сначала строится первый вектор ![]() , из его конца строится второй вектор
, из его конца строится второй вектор ![]() . Итоговый вектор
. Итоговый вектор ![]() проводится из начала первого к концу второго вектора.
проводится из начала первого к концу второго вектора.
Сложение двух векторов методом параллелограмма (рис.4б). Оба вектора ![]() строятся выходящими из одной точки. К концам векторов достраиваются две стороны параллелограмма. Итоговый вектор
строятся выходящими из одной точки. К концам векторов достраиваются две стороны параллелограмма. Итоговый вектор ![]() проводится из начала векторов к противоположной вершине параллелограмма.
проводится из начала векторов к противоположной вершине параллелограмма.
Сложение любого числа векторов (рис.5). Сначала строится первый вектор ![]() , из его конца строится второй вектор
, из его конца строится второй вектор ![]() , из конца второго третий
, из конца второго третий ![]() и далее строятся остальные векторы. Итоговый вектор
и далее строятся остальные векторы. Итоговый вектор ![]() проводится из начала первого вектора к концу самого последнего.
проводится из начала первого вектора к концу самого последнего.
Разность двух векторов (Рис.6). Оба вектора ![]() строятся выходящими из одной точки. Итоговый вектор
строятся выходящими из одной точки. Итоговый вектор ![]() соединяет концы векторов в направлении к уменьшаемому вектору
соединяет концы векторов в направлении к уменьшаемому вектору ![]() .
.